Courses by Software
Courses by Semester
Courses by Domain
Tool-focused Courses
Machine learning
POPULAR COURSES
Post Graduate Program in Hybrid Electric Vehicle Design and AnalysisPost Graduate Program in Computational Fluid DynamicsPost Graduate Program in CADPost Graduate Program in CAEPost Graduate Program in Manufacturing DesignPost Graduate Program in Computational Design and Pre-processingPost Graduate Program in Complete Passenger Car Design & Product DevelopmentSuccess Stories
Week 7 - Simulation of a 1D Super-sonic nozzle flow simulation using Macormack Method
AIM- Simulation of 1D supersonic nozzle flow simulation using Macormack method OBJECTIVES- 1. Steady-state distribution of primitive variables inside the nozzle2. Time-wise variation of the primitive variables3. Variation of Mass flow rate distribution inside the nozzle at different time steps during the time-marching…
Mainak Bhowmick
updated on 30 Sep 2020
AIM- Simulation of 1D supersonic nozzle flow simulation using Macormack method
OBJECTIVES-
1. Steady-state distribution of primitive variables inside the nozzle
2. Time-wise variation of the primitive variables
3. Variation of Mass flow rate distribution inside the nozzle at different time steps during the time-marching process
4. Comparison of Normalized mass flow rate distributions of both forms
THEORY
The steady ,isentropic flow through a convergent_divergent nozzle is considered.The flow at the inlet to the nozzle comes from a reservoir where the pressure and temperature are denoted by ρ0andT0ρ0andT0respectively.The area is large hence the velocity tends to zero. Thus the
ρ0andT0ρ0andT0are the stagnation values or the total pressure and total temperature respectively. The flow expands isentropically to supersonic speeds at the nozzle exit, where the exit pressure , temperature velocity and mach number are denoted byρe,Te,VeandMeρe,Te,VeandMerespectively. The flow is locally subsonic in the convergent section of the nozzle ,sonic at the throatand supersonic at the divergent section.
i.e. at M<1:subsonic
M=1:sonic
M>1:supersonic
FIG:-schematic diagram of supersonic- subsonic isentropic nozzle flow
GOVERNING EQUATIONS
Continuity:
ρ1V1A1=ρ2V2A2ρ1V1A1=ρ2V2A2
Momentum
ρ1V1A1+ρ1V21A1+∫A2A1p.dA=ρ2V2A2+ρ2V22A2ρ1V1A1+ρ1V21A1+∫A2A1p.dA=ρ2V2A2+ρ2V22A2
Energy
h1+V212=h2+V222h1+V212=h2+V222
SOLVING THE EQUATIONS ANALYTICALLY
AA⋅=1M2⋅[(2γ+1)⋅(1+γ-12⋅M2)]γ+1γ-1AA⋅=1M2⋅[(2γ+1)⋅(1+γ−12⋅M2)]γ+1γ−1
PP0=(1+γ-12⋅M2)-(γγ-1)PP0=(1+γ−12⋅M2)−(γγ−1)
ρρ0=(1+γ-12⋅M2)-(1γ-1)ρρ0=(1+γ−12⋅M2)−(1γ−1)
TT0=(1+γ-12⋅M2)-1TT0=(1+γ−12⋅M2)−1
TIME STEP USED FOR THE CODE
dt=c*(min(ΔXa+VΔXa+V))
NON CONSERVATIVE FORM OF EQUATION
CONTINUITY
∂ρ′A′∂t′+ρA′∂V′∂X′+ρ′V′∂A′∂X′+V′A′∂P′∂X′=0
MOMENTUM
ρ∂V′∂t′+ρV′∂V′∂X′=-R(ρ′∂T′∂X′+T′∂P′∂X′)
ENERGY
ρ′Cv∂T′∂t′+ρ′V′Cv∂T′∂X′=-ρ′RT′[∂V′∂X′+V′∂lnA′∂X′]
INPUTS
ρ=1-0.3146X
T=1-0.2314X
V=(0.1+1.09X)T12
CODE TO SOLVE NON CONSERVATIVE
function [rho, v, t, rho_t, v_t, t_t, M_t, p_t, m]=non_conservation(nt,n,x,gamma,c,a,dx,throat)
%calculation initial profiles
rho=1-0.3146*x;
t=1-0.2314*x;
v=(0.1+1.09*x).*t.^0.5;
dt=min(c.*dx./(sqrt(t).*v));
for k=1:nt
rho_old=rho;
t_old=t;
v_old=v;
%predictor method
for j=2:n-1
dvdx=(v(j+1)-v(j))/dx;
drhodx=(rho(j+1)-rho(j))/dx;
dtdx=(t(j+1)-t(j))/dx;
dlogadx=(log(a(j+1))-log(a(j)))/dx;
%continuity equation
drhodt_p(j)=-rho(j)*dvdx-rho(j)*v(j)*dlogadx-v(j)*drhodx;
%momentum equation
dvdt_p(j)=-v(j)*dvdx-(1/gamma)*(dtdx+(t(j)/rho(j))*drhodx);
%energy equation
dtdt_p(j)=-v(j)*dtdx-(gamma-1)*t(j)*(dvdx+v(j)*dlogadx);
%update
rho(j)=rho(j)+drhodt_p(j)*dt;
v(j)=v(j)+dvdt_p(j)*dt;
t(j)=t(j)+dtdt_p(j)*dt;
end
%corrector steps
for j=2:n-1
dvdx=(v(j)-v(j-1))/dx;
drhodx=(rho(j)-rho(j-1))/dx;
dtdx=(t(j)-t(j-1))/dx;
dlogadx=(log(a(j))-log(a(j-1)))/dx;
%continuity equation
drhodt_c(j)=-rho(j)*dvdx-rho(j)*v(j)*dlogadx-v(j)*drhodx;
%momentum equation
dvdt_c(j)=-v(j)*dvdx-(1/gamma)*(dtdx+(t(j)/rho(j))*drhodx);
%energy equation
dtdt_c(j)=-v(j)*dtdx-(gamma-1)*t(j)*(dvdx+v(j)*dlogadx);
end
%average time derivative
drhodt=0.5*(drhodt_c+ drhodt_p);
dvdt=0.5*(dvdt_c+dvdt_p);
dtdt=0.5*(dtdt_c+dtdt_p);
for i=2:n-1
%final solution update
v(i)=v_old(i)+dvdt(i)*dt;
rho(i)=rho_old(i)+drhodt(i)*dt;
t(i)=t_old(i)+dtdt(i)*dt;
end
%boundar conditions
%input
v(1)=2*v(2)-v(3);
%output
v(n)=2*v(n-1)-v(n-2);
rho(n)=2*rho(n-1)-rho(n-2);
t(n)=2*t(n-1)-t(n-2);
%defining pressure mass flow and mach number
p=rho.*t;
m=rho.*a.*v;
M=v./sqrt(t);
%for the throat
t_t(k)=t(throat);
p_t(k)=p(throat);
rho_t(k)=rho(throat);
v_t(k)=v(throat);
M_t(k)=M(throat);
m(k,:)=m(throat);
%plotting non dimensional distance vs mass
figure(1)
hold on
if k==50
plot(x,m,'b')
elseif k==100
plot(x,m,'g')
elseif k==150
plot(x,m,'y')
elseif k==200
plot(x,m,'m')
elseif k==700
plot(x,m,'c')
legend('50','100','150','200','700')
xlabel('nondimensional distance through nozzle')
ylabel('mass flow rate')
end
end
%plotting the time step non dimensional parameters
figure(2)
subplot(4,1,1)
plot(p_t,'m');
ylabel('P/P0');
subplot(4,1,2)
plot(t_t,'g');
ylabel('T/T0');
subplot(4,1,3)
plot(rho_t,'b')
ylabel('Density/Density0');
subplot(4,1,4)
% plot(M_throat,'r')
ylabel('Mlabel');
xlabel('no of time steps');
%plotting non dimensional distance vs mass
figure(3)
subplot(4,1,1)
plot(x,M,'b')
axis([0 3 0 4])
ylabel('Mach Number');
grid on;
subplot(4,1,2)
plot(x,p,'g');
axis([0 3 0 1.2])
ylabel('Pressure ratio');
grid on;
subplot(4,1,3)
plot(x,rho,'r');
axis([0 3 0 1.2])
ylabel('density ratio');
grid on;
subplot(4,1,4)
plot(x,t,'m');
axis([0 3 0 1.2])
ylabel('temperature');
xlabel('X');
grid on;
end
OUTPUT
QUALiTATIVE ASPECTS
Time wise variation of density machnumber pressure and temperature
NON DIMENSIONAL DISTANCE VS MASS FLOW RATE FOR DIFFERENT TIME STEP
CONSERVATIVE EQUATIONS
CONTINUITY
∂ρ′A′∂t′+∂ρ′A′∂x=0
MOMENTUM
∂ρ′A′V′∂t+∂[ρ′A′V′2+1γρ′A′)∂X=1γP′∂A′∂V′
ENERGY
∂(ρ′(e′γ-1+γ2V′2)A′)∂t′+∂ρ′(e′γ-1+γ2V′2)∂X′V′A′+ρ′A′V′=0
TO SOLVE THE EQUATIONS WE CONSIDER
U1=ρ′A′
U2=ρ′A′V′
U3=ρ′(e′γ-1+γ2V′2)A
f1=ρ′A′V′
f2=ρ′A′V′+1γρ′A′
f3=ρ′(e′γ-1+γ2V′2)V′A′+p′A′V′
J=1γρ′∂A′∂x′
FINAL EQUATIONS
∂U1∂(t′)=-∂F1∂X′
∂U2∂(t′)=-∂F2∂X′+J2
∂U3∂(t′)=-∂F3∂X′
INITIAL CONDITIONS
ρ′=1.0;T′=1.0-{0≤X′≤0.5}
ρ′=1.0-0.366(X′-0.5);T′=1.0-0.167(X′-0.5)-{0.5≤X′≤1.5}
ρ′=0.634-0.3879(X′-1.5);T′=0.833-0.3507(X′-1.5)-{1.5≤X′≤3.5}
function [rho, v, t,rho_th,v_th,t_th,M_th, p_th,m_th]=conservation(nt,n,x,gamma,c,a,dx,throat)
%initial values
for i=1:n
if (x(i)>=0 && x(i)<=0.5)
rho(i)=1;
t(i)=1;
elseif (x(i)>=0.5 && x(i)<=1.5)
rho(i)=1-0.366*(x(i)-0.5);
t(i)=1-0.167*(x(i)-0.5);
elseif (x(i)>=1.5 && x(i)<=3.5)
rho(i)=0.634-0.3879*(x(i)-1.5);
t(i)=0.8355-0.3507*(x(i)-1.5);
end
end
v=0.59./(rho.*a);
%timr step
dt=min(c.*dx./(sqrt(t)+v));
%Mackmorks technique for solving
U_1=rho.*a;
U_2=rho.*a.*v;
U_3=rho.*a.*((t./(gamma-1))+((gamma./2).*(v.^2)));
%time loop
for k=1:nt
U_old1=U_1;
U_old2=U_2;
U_old3=U_3;
f1=U_2;
f2=((U_2.^2)./U_1)+(((gamma-1)/gamma)*(U_3-((gamma/2)*((U_2.^2)./U_1))));
f3=((gamma*U_2.*U_3)./U_1)-(gamma*(gamma-1)*(U_2.^3))./(2*(U_1.^2));
%predictor step
for j=2:n-1
dadx=((a(j+1)-a(j)))/dx;
J2=rho(j)*t(j)*dadx/gamma;
%continuity equation
dudt1p(j)=-(f1(j+1)-f1(j))/dx;
%momentum equation
dudt2p(j)=-(f2(j+1)-f2(j))/dx+J2;
%energy
dudt3p(j)=-(f3(j+1)-f3(j))/dx;
%solution update
U_1(j)=U_1(j)+ dudt1p(j)*dt;
U_2(j)=U_2(j)+ dudt2p(j)*dt;
U_3(j)=U_3(j)+ dudt3p(j)*dt;
end
%Decoding the values
rho_p=U_1./a;
v_p=U_2./U_1;
t_p=(gamma-1)*((U_3./U_1)-((gamma/2)*(v_p.^2)));
v_p=U_2./U_1;
f1=U_2;
f2=((U_2.^2)./U_1)+(((gamma-1)/gamma)*(U_3-((gamma/2)*((U_2.^2)./U_1))));
f3=((gamma*U_2.*U_3)./U_1)-(gamma*(gamma-1)*(U_2.^3))./(2*(U_1.^2));
for j=2:n-1
dadx=((a(j)-a(j-1)))/dx;
J2=rho_p(j).*t_p(j).*dadx/gamma;
%continuity equation
dudt1c(j)=-(f1(j)-f1(j-1))/dx;
%momentum equation
dudt2c(j)=-(f2(j)-f2(j-1))/dx+J2;
%energy
dudt3c(j)=-(f3(j)-f3(j-1))/dx;
end
%average time step
dudt1=0.5*(dudt1p+dudt1c);
dudt2=0.5*(dudt2p+dudt2c);
dudt3=0.5*(dudt3p+dudt3c);
%final solution
for i=1:n-1
U_1(i)=U_old1(i)+dudt1(i)*dt;
U_2(i)=U_old2(i)+dudt2(i)*dt;
U_3(i)=U_old3(i)+dudt3(i)*dt;
end
%boundary conditions
%inlet
U_1(1)=rho_p(1).*a(1);
U_2(1)=2*U_2(2)-U_2(3);
v_p(1)=U_2(1)/U_1(1);
U_3(1)=U_1(1)*((t_p(1)/(gamma-1))+((gamma/2)*v_p(1).*v_p(1)^2));
%outlet
U_1(n)=2*U_1(n-1)-U_1(n-2);
U_2(n)=2*U_2(n-1)-U_2(n-2);
U_3(n)=2*U_3(n-1)-U_3(n-2);
%primitive variables decoding
rho=U_1./a;
v=U_2./U_1;
t=(gamma-1)*((U_3./U_1)-((gamma/2)*(v.^2)));
M=v./((t).^0.5);
p=rho.*t;
m(k,:)=rho.*v.*a;
%values at thrust
rho_th(k)=rho(throat);
v_th(k)=v(throat);
t_th(k)=t(throat);
M_th(k)=M(throat);
p_th(k)=p(throat);
m_th(k)=m(throat);
end
%plotting the time step non dimensional parameters
figure(1)
subplot(4,1,1)
plot(x,M,'r')
ylabel('Mach number')
subplot(4,1,2)
plot(x,p,'b')
ylabel('pressure')
subplot(4,1,3)
plot(x,rho,'c')
ylabel('density')
subplot(4,1,4)
plot(x,t,'g')
ylabel('temperature')
xlabel('X')
%plotting non dimensional distance vs mass
figure(2)
subplot(4,1,1)
plot(M_th,'r')
ylabel('mach number')
subplot(4,1,2)
plot(p_th,'c')
ylabel('pressure')
subplot(4,1,3)
plot(rho_th,'b')
ylabel('density')
subplot(4,1,4)
plot(t_th,'g')
ylabel('temperature')
xlabel('no of iterations')
end
OUTPUT
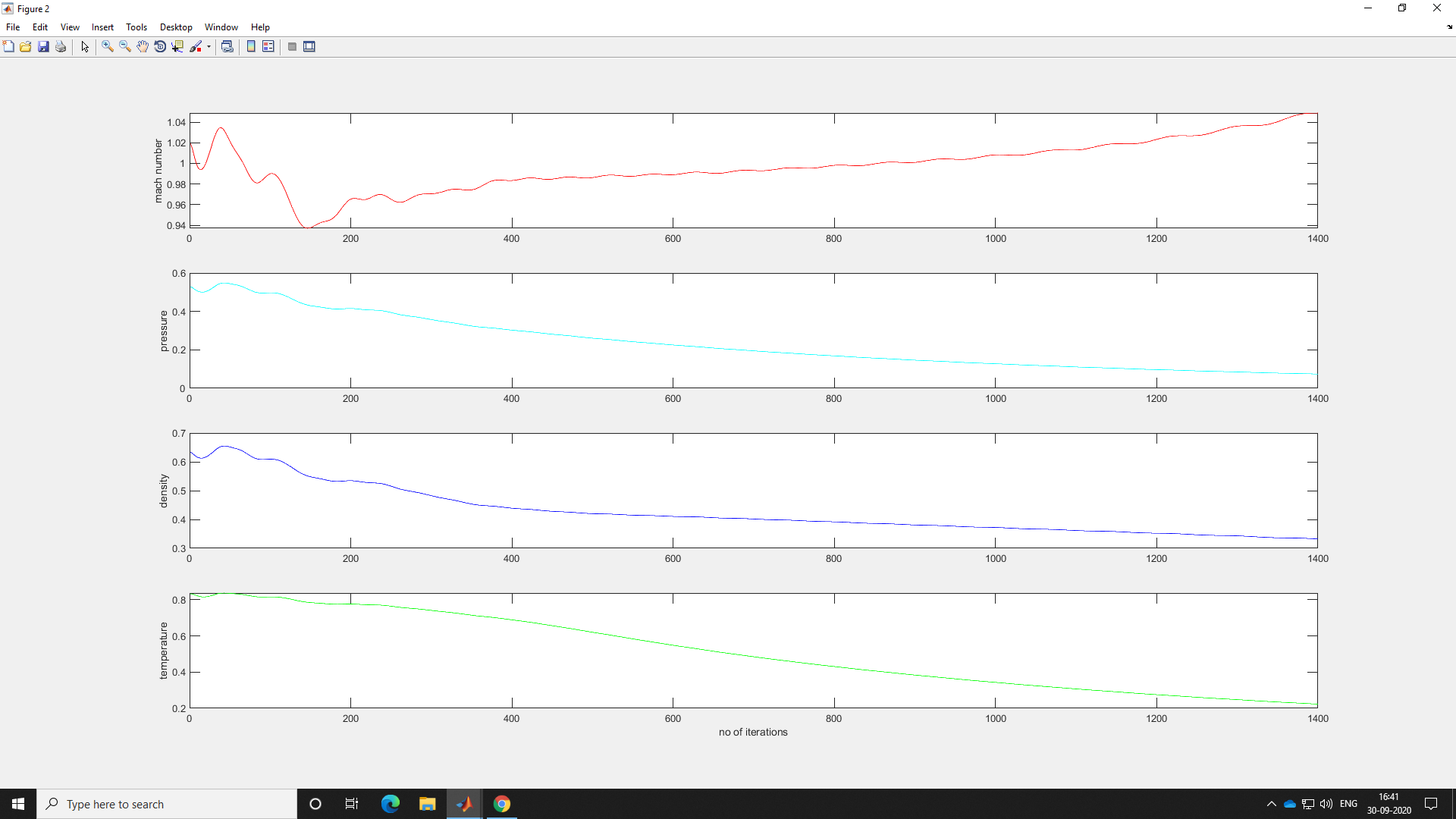
MAIN PROGRAM
clear all
close all
clc
%grid points
value_of_n=input('1 for 31 2 for 61:' );
if value_of_n==1
n=31;
elseif value_of_n==2
n=61;
end
%Length of
x=linspace(0,3,n);
dx=x(2)-x(1);
gamma=1.4;
c=.5;
a=1+2.2*(x-1.5).^2;
throat=(n+1)/2;
%time steps
nt=1400;
[rho_n, v_n, t_n, rho_th_n, v_th_n, t_th_n, M_th_n, p_th_n, m_n]=non_conservation(nt,n,x,gamma,c,a,dx,throat);
[rho_c, v_c, t_c, rho_th_c, v_th_c, t_th_c, M_th_c, p_th_c, m_c]=conservation(nt,n,x,gamma,c,a,dx,throat);
CALCULATING MASS FLOW WRT X
function [rho, v, t, rho_t, v_t, t_t, M_t, p_t, m_t,m]=non_conservation(nt,n,x,gamma,c,a,dx,throat)
%calculation initial profiles
rho=1-0.3146*x;
t=1-0.2314*x;
v=(0.1+1.09*x).*t.^0.5;
dt=min(c.*dx./(sqrt(t).*v));
for k=1:nt
rho_old=rho;
t_old=t;
v_old=v;
%predictor method
for j=2:n-1
dvdx=(v(j+1)-v(j))/dx;
drhodx=(rho(j+1)-rho(j))/dx;
dtdx=(t(j+1)-t(j))/dx;
dlogadx=(log(a(j+1))-log(a(j)))/dx;
%continuity equation
drhodt_p(j)=-rho(j)*dvdx-rho(j)*v(j)*dlogadx-v(j)*drhodx;
%momentum equation
dvdt_p(j)=-v(j)*dvdx-(1/gamma)*(dtdx+(t(j)/rho(j))*drhodx);
%energy equation
dtdt_p(j)=-v(j)*dtdx-(gamma-1)*t(j)*(dvdx+v(j)*dlogadx);
%update
rho(j)=rho(j)+drhodt_p(j)*dt;
v(j)=v(j)+dvdt_p(j)*dt;
t(j)=t(j)+dtdt_p(j)*dt;
end
%corrector steps
for j=2:n-1
dvdx=(v(j)-v(j-1))/dx;
drhodx=(rho(j)-rho(j-1))/dx;
dtdx=(t(j)-t(j-1))/dx;
dlogadx=(log(a(j))-log(a(j-1)))/dx;
%continuity equation
drhodt_c(j)=-rho(j)*dvdx-rho(j)*v(j)*dlogadx-v(j)*drhodx;
%momentum equation
dvdt_c(j)=-v(j)*dvdx-(1/gamma)*(dtdx+(t(j)/rho(j))*drhodx);
%energy equation
dtdt_c(j)=-v(j)*dtdx-(gamma-1)*t(j)*(dvdx+v(j)*dlogadx);
end
%average time derivative
drhodt=0.5*(drhodt_c+ drhodt_p);
dvdt=0.5*(dvdt_c+dvdt_p);
dtdt=0.5*(dtdt_c+dtdt_p);
for i=2:n-1
%final solution update
v(i)=v_old(i)+dvdt(i)*dt;
rho(i)=rho_old(i)+drhodt(i)*dt;
t(i)=t_old(i)+dtdt(i)*dt;
end
%boundar conditions
%input
v(1)=2*v(2)-v(3);
%output
v(n)=2*v(n-1)-v(n-2);
rho(n)=2*rho(n-1)-rho(n-2);
t(n)=2*t(n-1)-t(n-2);
%defining pressure mass flow and mach number
p=rho.*t;
m(k,:)=rho.*a.*v;
M=v./sqrt(t);
%for the throat
t_t(k)=t(throat);
p_t(k)=p(throat);
rho_t(k)=rho(throat);
v_t(k)=v(throat);
M_t(k)=M(throat);
m_t(k)=m(throat);
endfunction [rho, v, t,rho_th,v_th,t_th,M_th, p_th,m_th,m]=conservation(nt,n,x,gamma,c,a,dx,throat)
%initial values
for i=1:n
if (x(i)>=0 && x(i)<=0.5)
rho(i)=1;
t(i)=1;
elseif (x(i)>=0.5 && x(i)<=1.5)
rho(i)=1-0.366*(x(i)-0.5);
t(i)=1-0.167*(x(i)-0.5);
elseif (x(i)>=1.5 && x(i)<=3.5)
rho(i)=0.634-0.3879*(x(i)-1.5);
t(i)=0.8355-0.3507*(x(i)-1.5);
end
end
v=0.59./(rho.*a);
%timr step
dt=min(c.*dx./(sqrt(t)+v));
%Mackmorks technique for solving
U_1=rho.*a;
U_2=rho.*a.*v;
U_3=rho.*a.*((t./(gamma-1))+((gamma./2).*(v.^2)));
%time loop
for k=1:nt
U_old1=U_1;
U_old2=U_2;
U_old3=U_3;
f1=U_2;
f2=((U_2.^2)./U_1)+(((gamma-1)/gamma)*(U_3-((gamma/2)*((U_2.^2)./U_1))));
f3=((gamma*U_2.*U_3)./U_1)-(gamma*(gamma-1)*(U_2.^3))./(2*(U_1.^2));
%predictor step
for j=2:n-1
dadx=((a(j+1)-a(j)))/dx;
J2=rho(j)*t(j)*dadx/gamma;
%continuity equation
dudt1p(j)=-(f1(j+1)-f1(j))/dx;
%momentum equation
dudt2p(j)=-(f2(j+1)-f2(j))/dx+J2;
%energy
dudt3p(j)=-(f3(j+1)-f3(j))/dx;
%solution update
U_1(j)=U_1(j)+ dudt1p(j)*dt;
U_2(j)=U_2(j)+ dudt2p(j)*dt;
U_3(j)=U_3(j)+ dudt3p(j)*dt;
end
%Decoding the values
rho_p=U_1./a;
v_p=U_2./U_1;
t_p=(gamma-1)*((U_3./U_1)-((gamma/2)*(v_p.^2)));
v_p=U_2./U_1;
f1=U_2;
f2=((U_2.^2)./U_1)+(((gamma-1)/gamma)*(U_3-((gamma/2)*((U_2.^2)./U_1))));
f3=((gamma*U_2.*U_3)./U_1)-(gamma*(gamma-1)*(U_2.^3))./(2*(U_1.^2));
for j=2:n-1
dadx=((a(j)-a(j-1)))/dx;
J2=rho_p(j).*t_p(j).*dadx/gamma;
%continuity equation
dudt1c(j)=-(f1(j)-f1(j-1))/dx;
%momentum equation
dudt2c(j)=-(f2(j)-f2(j-1))/dx+J2;
%energy
dudt3c(j)=-(f3(j)-f3(j-1))/dx;
end
%average time step
dudt1=0.5*(dudt1p+dudt1c);
dudt2=0.5*(dudt2p+dudt2c);
dudt3=0.5*(dudt3p+dudt3c);
%final solution
for i=1:n-1
U_1(i)=U_old1(i)+dudt1(i)*dt;
U_2(i)=U_old2(i)+dudt2(i)*dt;
U_3(i)=U_old3(i)+dudt3(i)*dt;
end
%boundary conditions
%inlet
U_1(1)=rho_p(1).*a(1);
U_2(1)=2*U_2(2)-U_2(3);
v_p(1)=U_2(1)/U_1(1);
U_3(1)=U_1(1)*((t_p(1)/(gamma-1))+((gamma/2)*v_p(1).*v_p(1)^2));
%outlet
U_1(n)=2*U_1(n-1)-U_1(n-2);
U_2(n)=2*U_2(n-1)-U_2(n-2);
U_3(n)=2*U_3(n-1)-U_3(n-2);
%primitive variables decoding
rho=U_1./a;
v=U_2./U_1;
t=(gamma-1)*((U_3./U_1)-((gamma/2)*(v.^2)));
M=v./((t).^0.5);
p=rho.*t;
m(k,:)=rho.*v.*a;
%values at thrust
rho_th(k)=rho(throat);
v_th(k)=v(throat);
t_th(k)=t(throat);
M_th(k)=M(throat);
p_th(k)=p(throat);
m_th(k)=m(throat);
end
clear all
close all
clc
%grid points
value_of_n=input('1 for 31 2 for 61:' );
if value_of_n==1
n=31;
elseif value_of_n==2
n=61;
end
%Length of
x=linspace(0,3,n);
dx=x(2)-x(1);
gamma=1.4;
c=.5;
a=1+2.2*(x-1.5).^2;
throat=(n+1)/2;
%time steps
nt=1400;
[rho_n, v_n, t_n, rho_th_n, v_th_n, t_th_n, M_th_n, p_th_n, m_n,mn]=non_conservation(nt,n,x,gamma,c,a,dx,throat);
[rho_c, v_c, t_c, rho_th_c, v_th_c, t_th_c, M_th_c, p_th_c, m_c,mc]=conservation(nt,n,x,gamma,c,a,dx,throat);
for i=1:nt
figure(1)
plot(x,mn(1,:),'b',x,mc(1,:),'r')
xlabel('X/L');
ylabel('mass flow rate')
endOUTPUT
CONCLUSION
1. The conservative form does a better job in of preserving the mass throughout the flowfield.
2. Conservative requires more work.
3. The non conservative lower residuals.
Leave a comment
Thanks for choosing to leave a comment. Please keep in mind that all the comments are moderated as per our comment policy, and your email will not be published for privacy reasons. Please leave a personal & meaningful conversation.
Other comments...
Be the first to add a comment
Read more Projects by Mainak Bhowmick (6)
Week 11 - Simulation of Flow through a pipe in OpenFoam
AIM- Write a program in Matlab that can generate the computational mesh automatically for any wedge angle and grading schemes For a baseline mesh, show that the velocity profile matches with the Hagen poiseuille's equation Show that the velocity profile is fully developed Post process velocity and shear stress…
29 Oct 2020 06:38 PM IST
Week 9 - FVM Literature Review
FINITE VOLUME METHOD - The finite volume is a discretisation method which is well suited for numerical simulations of various types namely hyperbolic, elliptic and parabolic for instance of conservation laws. It has been extensively used in several engineering fields, such as fluid mechanics, heat and mass transfer or…
20 Oct 2020 10:43 AM IST
Week 8 - BlockMesh Drill down challenge
AIM-to create a BlockMesh and to simulate it . OBJECTIVES:- How does the velocity magnitude profile change as a function of mesh grading factor. Use factors, 0.2, 0.5,0.8 Measure the velocity profile at 0.085 m from the inlet of the geometry Plot must be a line plot Compare velocity magnitude contours near the step region…
15 Oct 2020 09:58 AM IST
Week 7 - Simulation of a 1D Super-sonic nozzle flow simulation using Macormack Method
AIM- Simulation of 1D supersonic nozzle flow simulation using Macormack method OBJECTIVES- 1. Steady-state distribution of primitive variables inside the nozzle2. Time-wise variation of the primitive variables3. Variation of Mass flow rate distribution inside the nozzle at different time steps during the time-marching…
30 Sep 2020 08:16 PM IST
Related Courses
0 Hours of Content
Skill-Lync offers industry relevant advanced engineering courses for engineering students by partnering with industry experts.
Our Company
4th Floor, BLOCK-B, Velachery - Tambaram Main Rd, Ram Nagar South, Madipakkam, Chennai, Tamil Nadu 600042.
Top Individual Courses
Top PG Programs
Skill-Lync Plus
Trending Blogs
© 2025 Skill-Lync Inc. All Rights Reserved.