Week 11 - Simulation of Flow through a pipe in OpenFoam
AIM-
- Write a program in Matlab that can generate the computational mesh automatically for any wedge angle and grading schemes
- For a baseline mesh, show that the velocity profile matches with the Hagen poiseuille's equation
- Show that the velocity profile is fully developed
- Post process velocity and shear stress
Hagen poiseuille's equation
The Hagen–Poiseuille Equation is a fluidic law to calculate flow pressure drop in a long cylindrical pipe.
`DeltaP=(8*mu*L*Q)/(pi*R^4)`
`Q=A*V`
`A=r^2`
`DeltaP=(8*mu*L*V)/(pi*r^2)`
Reynold's Number
it is the ratio of inertia force to viscous force.
`Re=(rho*V*D)/mu`
Laminar Flow
Flow having a Reynolds number 1500-2000 is called a Laminar Flow.
Critical value for Reynolds number is approximately 2040 thus for the simulation 2040 is used.
Kinematic Pressure Difference
It is the ratio of normal pressure difference and the density of fluid.
`DeltaPunderset(ke)()=(DeltaP)/rho`
Shear Stress
Defined as the force per unit area.
`tau=(2*mu*Vunderset(max)()*R)/r^2`
`Vunderset(max)()=2*Vunderset(avg)()`
Entrance Length
The hydrodynamic entrance region refers to the area of a pipe where fluid entering a pipe develops a velocity profile due to propagating from the interior wall of a pipe. This region is characterized by a non-uniform flow.The fluid enters a pipe at a uniform velocity, then fluid particles in the layer in contact with the surface of the pipe come to a complete stop due to the no slip condition.Due to viscous forces within the fluid, the layer in contact with the pipe surface resists the motion of adjacent layers and slows adjacent layers of fluid down gradually, forming a velocity profile. For the conservation of massto hold true, the velocity of layers of the fluid in the center of the pipe increases to compensate for the reduced velocities of the layers of fluid near the pipe surface. This develops a velocity gradient across the cross section of the pipe.
image source:-Wikipedia
Entrance length=0.06*Re*D
OPEN FOAM BOUNDARIES USED
PATCH-The basic patch type for a patch condition that contains no geometric or topological information about the mesh (with the exception of wall), e.g. an inlet or an outlet.
Wedge-There are instances where a patch that coincides with a wall needs to be identifiable as such, particularly where specialist modelling is applied at wall boundaries. A good example is wall turbulence modelling where a wall must be specified with a wall patch type, so that the distance from the wall of the cell centres next to the wall are stored as part of the patch.
Empty-While OpenFOAM always generates geometries in 3 dimensions, it can be instructed to solve in 2 (or 1) dimensions by specifying a special empty condition on each patch whose plane is normal to the 3rd (and 2nd) dimension for which no solution is required.
Variables
Reynold's Number=2040
Density of water=1000 `(kg)/m^3`
Diameter =0.0005 m
L=1.3120 m
dynamic viscosity=9e-4
BLOCKMESH CODE:
clear all
close all
clc
%reynolds number
re=2040;
%density
rho=1000;
%Diameter
D=0.005;
%radius
r=D/2;
%entrance length
Le=0.06*re*D;
%length
L=0.7+Le;
%dynamic viscosity
mu=9e-4;
v=(re*9e-4)/(D*1000);
vmax=2*v;
theta=4;
y=r*cosd(theta/2);
z=r*sind(theta/2);
%Shear stress calculation
R=linspace(0,r,100);
for i=1:length(R)
shear(i)=2*vmax*mu*(R(i))/(r^2);
end
plot(shear,R);
xlabel('radius')
ylabel('shear stress')
bmd=fopen('blockMeshDict.txt','w');%w stands for write
fprintf(bmd,'%s','/*--------------------------------*- C++ -*----------------------------------*\');
fprintf(bmd,'\n ========= |\n');
fprintf(bmd,' \\ / F ield | OpenFOAM: The Open Source CFD Toolbox\n');
fprintf(bmd,' \\ / O peration | Website: https://openfoam.org\n');
fprintf(bmd,' \\ / A nd | Version: 8\n');
fprintf(bmd,' \\/ M anipulation |\n');
fprintf(bmd,'%s','\*---------------------------------------------------------------------------*/');
fprintf(bmd,'\nFoamFile\n');
fprintf(bmd,'{\n');
fprintf(bmd,'version 2.0;\n');
fprintf(bmd,' format ascii;\n');
fprintf(bmd,' class dictionary;\n');
fprintf(bmd,' object blockMeshDict;\n');
fprintf(bmd,'}\n');
fprintf(bmd,'// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //\n');
fprintf(bmd,'\n');
fprintf(bmd,'convertToMeters 1;');
%part of program to find the vertces
fprintf(bmd,'\nvertices\n');
fprintf(bmd,'(\n');
fprintf(bmd,'\t(0 0 0)//0\n');%0
fprintf(bmd,'\t(%d %d %d)//1\n',0, y, z);%1
fprintf(bmd,'\t(%d %d %d)//2\n',0, y, -z);%2
fprintf(bmd,'\t(%d %d %d)//3\n',L, 0, 0);%3
fprintf(bmd,'\t(%d %d %d)//4\n',L, y, z);%4
fprintf(bmd,'\t(%d %d %d)//5\n',L, y, -z);%5
fprintf(bmd,');');
%part of program to find the blocks
fprintf(bmd,'\nblocks');
fprintf(bmd,'\n(');
fprintf(bmd,'\n\thex (0 3 5 2 0 3 4 1) (20 20 1) simpleGrading (1 0.5 1)');
fprintf(bmd,'\n);');
fprintf(bmd,'\n\nedges');
fprintf(bmd,'\n(\n);');
fprintf(bmd,'\n');
%Boundary
fprintf(bmd,'\nboundary');
fprintf(bmd,'\n(');
%inlet
fprintf(bmd,' \n\tinlet');
fprintf(bmd,'\n\t{');
fprintf(bmd,'\n\t\ttype patch;');
fprintf(bmd,'\n\t\tfaces');
fprintf(bmd,'\n\t\t(');
fprintf(bmd,'\n\t\t\t(0 1 2 0)');
fprintf(bmd,'\n\t\t);');
fprintf(bmd,'\n\t\t}');
fprintf(bmd,'\n');
%outlet
fprintf(bmd,' \n\toutlet');
fprintf(bmd,'\n\t{');
fprintf(bmd,'\n\t\ttype patch;');
fprintf(bmd,'\n\t\tfaces');
fprintf(bmd,'\n\t\t(');
fprintf(bmd,'\n\t\t\t(3 5 4 3)');
fprintf(bmd,'\n\t\t);');
fprintf(bmd,'\n\t}');
fprintf(bmd,'\n');
%Top
fprintf(bmd,' \n\ttop');
fprintf(bmd,'\n\t{');
fprintf(bmd,'\n\t\ttype wall;');
fprintf(bmd,'\n\t\tfaces');
fprintf(bmd,'\n\t\t(');
fprintf(bmd,'\n\t\t\t(1 4 5 2)');
fprintf(bmd,'\n\t\t);');
fprintf(bmd,'\n\t}');
fprintf(bmd,'\n');
%Front
fprintf(bmd,' \n\tfront');
fprintf(bmd,'\n\t{');
fprintf(bmd,'\n\t\ttype wedge;');
fprintf(bmd,'\n\t\tfaces');
fprintf(bmd,'\n\t\t(');
fprintf(bmd,'\n\t\t\t(0 3 4 1)');
fprintf(bmd,'\n\t\t);');
fprintf(bmd,'\n\t}');
fprintf(bmd,'\n');
%back
fprintf(bmd,' \n\tback');
fprintf(bmd,'\n\t{');
fprintf(bmd,'\n\ttype wedge;');
fprintf(bmd,'\n\tfaces');
fprintf(bmd,'\n\t\t(');
fprintf(bmd,'\n\t\t\t(0 2 5 3)');
fprintf(bmd,'\n\t\t);');
fprintf(bmd,'\n\t}');
fprintf(bmd,'\n');
%axis
fprintf(bmd,' \n\taxis');
fprintf(bmd,'\n\t{');
fprintf(bmd,'\n\t\ttype empty;');
fprintf(bmd,'\n\t\tfaces');
fprintf(bmd,'\n\t\t(');
fprintf(bmd,'\n\t\t\t(0 3 3 0)');
fprintf(bmd,'\n\t\t);');
fprintf(bmd,'\n\t}');
fprintf(bmd,'\n);');
fprintf(bmd,'\nmergePatchPairs');
fprintf(bmd,'\n(\n);');
fprintf(bmd,'\n\t\t*--------------------------------**----------------------------------*');TRANSPORT PROPERTIES
/*--------------------------------*- C++ -*----------------------------------*\
========= |
\ / F ield | OpenFOAM: The Open Source CFD Toolbox
\ / O peration | Website: https://openfoam.org
\ / A nd | Version: 8
\/ M anipulation |
\*---------------------------------------------------------------------------*/
FoamFile
{
version 2.0;
format ascii;
class dictionary;
object blockMeshDict;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
convertToMeters 1;
vertices
(
(0 0 0)//0
(0 2.498477e-03 8.724874e-05)//1
(0 2.498477e-03 -8.724874e-05)//2
(1.312000e+00 0 0)//3
(1.312000e+00 2.498477e-03 8.724874e-05)//4
(1.312000e+00 2.498477e-03 -8.724874e-05)//5
);
blocks
(
hex (0 3 5 2 0 3 4 1) (20 20 1) simpleGrading (1 0.5 1)
);
edges
(
);
boundary
(
inlet
{
type patch;
faces
(
(0 1 2 0)
);
}
outlet
{
type patch;
faces
(
(3 5 4 3)
);
}
top
{
type wall;
faces
(
(1 4 5 2)
);
}
front
{
type wedge;
faces
(
(0 3 4 1)
);
}
back
{
type wedge;
faces
(
(0 2 5 3)
);
}
axis
{
type empty;
faces
(
(0 3 3 0)
);
}
);
mergePatchPairs
(
);
*--------------------------------**----------------------------------*VELOCITY
/*--------------------------------*- C++ -*----------------------------------*\
========= |
\\ / F ield | OpenFOAM: The Open Source CFD Toolbox
\\ / O peration | Website: https://openfoam.org
\\ / A nd | Version: 8
\\/ M anipulation |
\*---------------------------------------------------------------------------*/
FoamFile
{
version 2.0;
format ascii;
class volVectorField;
object U;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
dimensions [0 1 -1 0 0 0 0];
internalField uniform (0.3672 0 0);
boundaryField
{
inlet
{
type fixedValue;
value uniform (0.3672 0 0);
}
outlet
{
type zeroGradient;
}
axis
{
type empty;
}
top
{
type fixedValue;
value uniform (0 0 0);
}
front
{
type wedge;
}
back
{
type wedge;
}
}
// ************************************************************************* //PRESSURE
/*--------------------------------*- C++ -*----------------------------------*\
========= |
\\ / F ield | OpenFOAM: The Open Source CFD Toolbox
\\ / O peration | Website: https://openfoam.org
\\ / A nd | Version: 8
\\/ M anipulation |
\*---------------------------------------------------------------------------*/
FoamFile
{
version 2.0;
format ascii;
class volScalarField;
object p;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
dimensions [0 2 -2 0 0 0 0];
internalField uniform 0;
boundaryField
{
inlet
{
type zeroGradient;
}
outlet
{
type fixedValue;
value uniform 1.72;
}
axis
{
type empty;
}
top
{
type zeroGradient;
}
back
{
type wedge;
}
front
{
type wedge;
}
}
// ************************************************************************* //CONTROLDICT
/*--------------------------------*- C++ -*----------------------------------*\
========= |
\\ / F ield | OpenFOAM: The Open Source CFD Toolbox
\\ / O peration | Website: https://openfoam.org
\\ / A nd | Version: 8
\\/ M anipulation |
\*---------------------------------------------------------------------------*/
FoamFile
{
version 2.0;
format ascii;
class dictionary;
location "system";
object controlDict;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
application icoFoam;
startFrom startTime;
startTime 0;
stopAt endTime;
endTime 1;
deltaT 0.00001;
writeControl timeStep;
writeInterval 20;
purgeWrite 0;
writeFormat ascii;
writePrecision 6;
writeCompression off;
timeFormat general;
timePrecision 6;
runTimeModifiable true;
// ************************************************************************* //
CONTROLDICT
/*--------------------------------*- C++ -*----------------------------------*\
========= |
\\ / F ield | OpenFOAM: The Open Source CFD Toolbox
\\ / O peration | Website: https://openfoam.org
\\ / A nd | Version: 8
\\/ M anipulation |
\*---------------------------------------------------------------------------*/
FoamFile
{
version 2.0;
format ascii;
class dictionary;
location "constant";
object transportProperties;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
nu [0 2 -1 0 0 0 0] 0.01;
// ************************************************************************* //SHEAR STRESS
MESH
at point = 0.01m from the initial point
at point = 0.5 m from the initial point
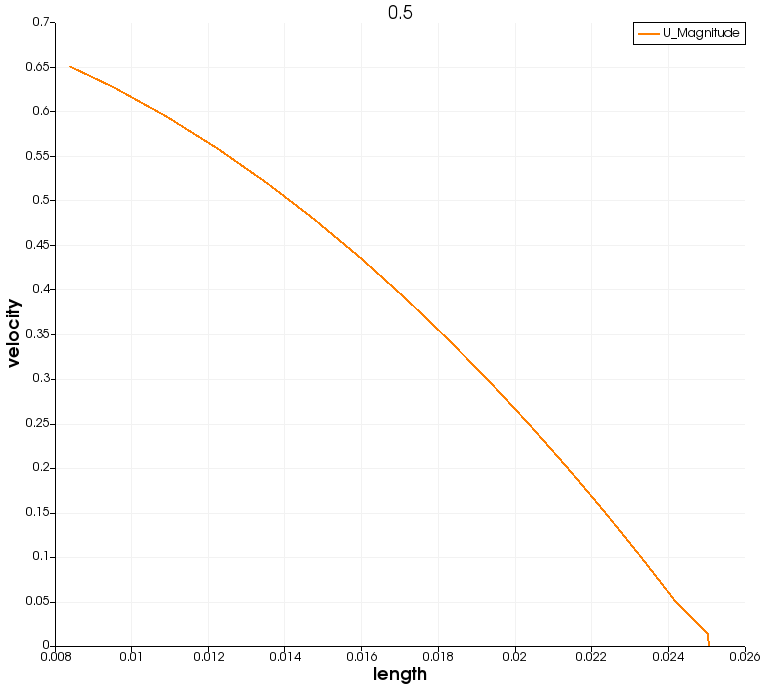
at point = 1m from the initial point
