Tensors, Stress, and 2D Meshing: A Primer for Beginners

A tensor is a mathematical object that describes a geometric relationship between vectors, scalars, and other tensors. They describe physical quantities with both magnitude and direction, such as velocity, force, and stress. 

In this blog, let us look at why stress is a tensor, what a plain stress condition and how it is related to 2D meshing.

Before jumping to the scientific definition, studying tensors in relation to vectors would be helpful. Vectors are those quantities that are described using both magnitude and direction. E.g., Velocity

This means that a vector can be represented using a line, which lies in a particular plane, as shown below:

Thus a particular vector is unidirectional and lies in a plane in space. On the other hand, a tensor is a 3-dimensional quantity, meaning it has a volumetric distribution in multiple directions. To visualize it better, consider a color dropped in a glass of water, as represented below.

     Image 2: Colour in water is distributed in all directions

The color is distributed in all directions, although not uniformly. A tensor also has a similar distribution in space. In simple terms, we can visualize this 3-dimensional distribution as a bundle of vectors related to each other by a definite relationship. This will allow us to understand the scientific definition of a tensor better.

Thus tensor is defined as an object that describes a relationship between sets of vectors in a vector space.

This brings us to the next question: why is stress a tensor?

Image 3: Conceptual representation of chemical bonds among particles of a material

Stress is the internal resistance offered by an object to its deformation. This is under the internal chemical bonds among the atoms/molecules of the object. So if a particular atom/molecule is deformed, the forces of attraction from the neighboring atoms/molecules will exert a resistive force, basically, the stress. 

But since the neighboring atoms are distributed in a 3-dimensional space, the forces of resistance are also distributed in a 3-dimensional space in a definite relationship with one another. Since force is a vector, the bundle of all these force vectors creates a tensor.

Image 4: 3D Stress distribution within a part 

The above image shows how stress is distributed in a 3-dimensional space in the object.

Because stress is a tensor, there are different ways to represent it. It can be expressed as matrix, a Mohr’s circle, von mises stress, or as normal and shear stresses separately.

Image 5: Normal stress, shear stress, and stress matrix

One approximation commonly used to simplify the representation and calculation of stress is called the plane stress condition.

In plane stress conditions, the normal and shear stresses directed perpendicular to a particular plane are assumed to be zero. This means, in the plane stress condition, the stress is assumed to be distributed in only one plane.  E.g. the stress in the z-direction is assumed to be zero. This makes many of the terms in the stress matrix zero, which makes calculations easier.

To imagine the plain stress condition, just assume that an object comprises thin slices arranged on top of another. If we consider any one of the slices, the stress in that slice will be distributed in the plane of that slice only, as the thickness is very small compared to other two dimensions. The stress in the direction normal to the plane of the slice will be zero.

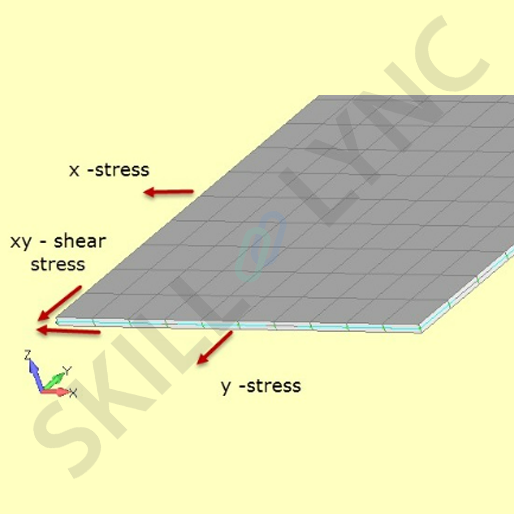
Image 6: Pictorial representation of plane stress conditions in XY plane

But what is the practical significance of plane stress conditions?

In FEA, to accurately analyze the state of a material, it's important to create a finite element mesh on the model. This process involves dividing the part into smaller elements and defining their behavior. 2D meshing involves creating a mesh in a single plane. Many thin components mesh using 2D elements like quad or tria. These 2D elements work on the principle of plain stress, under which stress normal to the plane of the elements is assumed to be zero.

This has 2 advantages:

Many of the terms in the stress matrix become zero, making calculations easier.

Two, the number of nodes under calculation is lesser than that in 3D meshing. In FEA, nodes are the points at which the edges of the elements intersect with each other. In layman's terms, they can be understood as the vertices of the elements. In 2D meshing, a linear quad element has 4 nodes. But the corresponding 3D element is the linear hexahedral or brick element, which has 8 nodes, as shown in the next image:

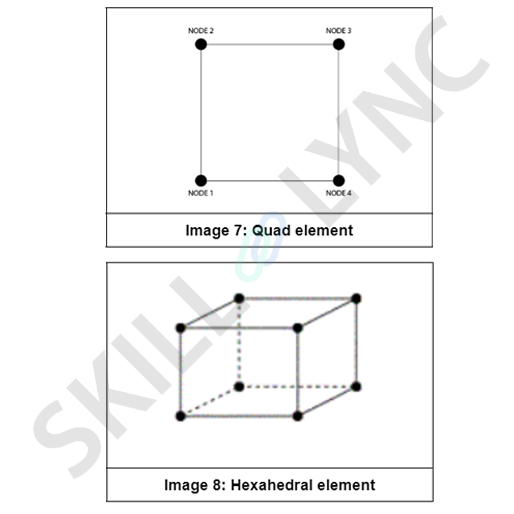
As a result, the calculation time is reduced, and we get faster results with reasonable accuracy.

So if you think about it, one of the basic engineering principles has become a foundational principle of FEA. In the image below, a sheet metal part, meshed using 2D elements is shown:

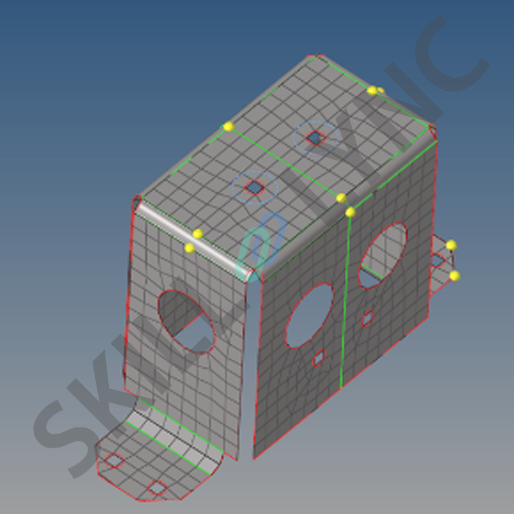
Image 9: the 2D meshing of a sheet metal part

This explains how tensors are related to plain stress conditions and 2D meshing. Understanding these concepts is crucial for accurately analyzing the behavior of models and ensuring their safety and stability.